Czy istnieje możliwość stworzenia modelu, który będzie dostarczał idealną krótkoterminową prognozę pogody? To podstawowe pytanie, jakie zadaje sobie każdy użytkownik prognoz meteorologicznych. Odpowiedź jest natychmiastowa, nie. Drugie pytanie, jakie w związku z tym się rodzi to dlaczego? Przyczyn jest wiele – błędy i niepewności pomiarowe, błędy obliczeniowe, dokładność zastosowanych schematów numerycznych, rozdzielczość siatek obliczeniowych oraz uproszczenie opisu procesów fizycznych zachodzących w atmosferze. Ale na początek należy odpowiedzieć na pytanie, czym jest model numerycznych prognoz pogody.
AUTORZY:
Mariusz J. Figurski, IMGW-PIB/Centrum Modelowania Meteorologicznego
Grzegorz Duniec, IMGW-PIB/Centrum Modelowania Meteorologicznego
Adam Jaczewski, IMGW-PIB/Centrum Modelowania Meteorologicznego
Model to nic innego jak program komputerowy, dość złożony, który potrafi symulować skomplikowane procesy fizyczne zachodzące w atmosferze. Stworzenie takiego modelu to długotrwały i trudny proces, wymagający wysokiej klasy specjalistów zarówno z zakresu fizyki atmosfery, jak i informatyki. Uproszczona procedura konstrukcji modelu przebiega następująco. Na początku należy przeanalizować procesy fizyczne zachodzące w atmosferze. Następnie opisać procesy dynamiczne i termodynamiczne przy pomocy języka matematyki, tj. równaniami. W kolejnym kroku należy dobrać odpowiednie schematy numeryczne, dzięki którym uzyska się rozwiązanie tych równań. Wówczas przygotowany zostaje program komputerowy, czyli tzw. kod, który dzięki wykorzystaniu superkomputera umożliwia symulację procesów fizycznych zachodzących w atmosferze w przyszłości. Tak ostatecznie powstaje numeryczna prognoza pogody.
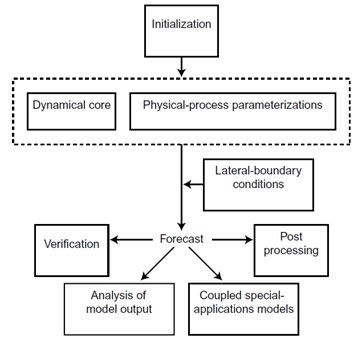
Błędy wynikające z warunków początkowych
Złożone procesy fizyczne zachodzące w atmosferze opisane są równaniami różniczkowymi. Aby otrzymać rozwiązanie tych równań, konieczne są warunki początkowe, czyli tzw. dane wejściowe, takie jak na przykład temperatura powietrza, temperatura punktu rosy, ciśnienie atmosferyczne, pole wiatru itd. Dane wejściowe do modelu pochodzą z pomiarów naziemnych, sondażowych i satelitarnych oraz uzupełniane są obserwacjami wykonywanymi na pokładach samolotów pozwalającymi zwiększyć ilość obserwacji 3D. Z metrologii wiadomo, że każdy pomiar obarczony jest błędem. Dane zbierane są różnymi technikami pomiarowymi bezpośrednimi i teledetekcyjnymi. Urządzenia pomiarowe, nawet te mierzące podstawowe pola meteorologiczne, mogą działać nieprawidłowo i tym samym rejestrować wielkości, które nie reprezentują rzeczywistości. Błędy instrumentalne występują we wszystkich pomiarach i są praktycznie nieuniknione. Zatem nie ma możliwości otrzymania idealnego odwzorowania początkowego stanu atmosfery, co będzie miało wpływ na symulację, czyli na prognozę.
W systemach „chaotycznych”, jakim niewątpliwe jest atmosfera ziemska, każda niedoskonałość inicjalizacji ma bardzo poważny wpływ na końcowy wynik symulacji. Oczywiście mowa tu o „teorii chaosu”, która zasadniczo sprowadza się do idei, że zmiany, nawet niewielkie, warunków początkowych mogą spowodować różną ewolucję systemu. W literaturze popularnej jako metafory teorii chaosu używa się dość często pojęcia „efekt motyla”. Sugeruje ono, że pozornie przypadkowe trzepotanie skrzydeł motyla w dowolniej części świata może ostatecznie wpłynąć na pogodę w innej części świata. Zagadnieniem tym zajmował się w drugiej połowie XX wieku Edward Lorentz, który pracował nad numerycznym prognozowaniem pogody. Podążając tropem Lorentza, można przeprowadzić eksperyment numeryczny polegający na tym, że do inicjalizacji obliczeń zostanie wykorzystany zestaw dwóch danych wejściowych różniących się dokładnością. Niech jeden zestaw zawiera dane początkowe z dokładnością do czterech miejsc po przecinku, a drugi z dokładnością do dwóch miejsc po przecinku. Po przeprowadzeniu obliczeń, ze zdziwieniem zostanie stwierdzone, że otrzymane dwie symulacje różnią się od siebie. Co więcej, rozbieżności w symulacji będą narastały z upływem czasu symulacji. Można z tego wnioskować, że zachowanie naszego układu będzie zależało od warunków początkowych, a dokładniej zachowanie układu będzie bardzo wrażliwe na warunki początkowe.
Z przeprowadzone eksperymentu numerycznego wynika, że nawet niewielkie, rzędu kilku dziesiątych procenta czy promila, różnice w danych wejściowych prowadzą do różnych scenariuszy procesów fizycznych w atmosferze. Im bardziej dane wejściowe będą różniły się od rzeczywistych chwilowych warunków meteorologicznych, tym wynik symulacji będzie dalszy od rzeczywistego stanu atmosfery. Ponieważ chwilowe dane opisujące aktualny stan atmosfery nie są dokładne, otrzymanie prawidłowej symulacji procesów fizycznych w atmosferze w dłuższych horyzoncie czasu, np. prognozy średnioterminowej, nie jest możliwe. W celu poprawy jakości prognoz numerycznych stosuje się tzw. asymilację danych, która wykorzystuje bieżące dane obserwacyjne stanu atmosfery. Tak otrzymane dane wejściowe poprawiają prognozę krótkoterminową.
Błędy obliczeniowe i dokładność schematów różnicowych
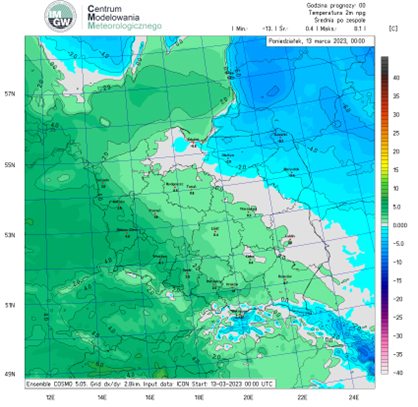
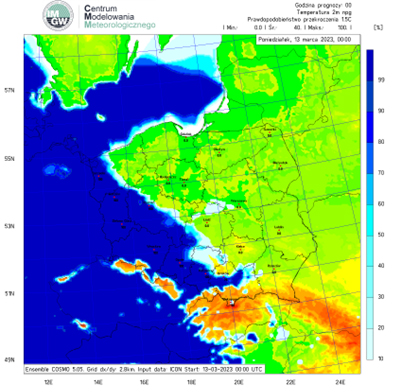
Problemy z modelowaniem nie kończą się wraz z procedurą inicjalizacji. Ważną grupę błędów stanowią metody wykonywania obliczeń na superkomputerach. Pierwszym przykładem, który należy wymienić, to błędy zaokrąglania liczb, np. zaokrąglenie 29,999999 stopni Celsjusza do 30 stopni może mieć znaczenie, a błędy tego typu są sumowane zgodnie z prawem przenoszenia błędów. Różne komputery mogą przeprowadzać obliczenia z różną dokładnością po przecinku. W celu otrzymania prognostycznych wartości pól meteorologicznych w określonym czasie, musi zostać przeprowadzone wiele obliczeń pośrednich. Aby model był stabilny, krok czasowy obliczeń jest znacząco mniejszy od 1 godziny, a tym bardziej od 3 godzin. Wartość kroku czasowego obliczeń zależy od rozdzielczości siatki. Wraz ze wzrostem rozdzielczości, krok czasowy obliczeń maleje. Chcąc otrzymać obliczone wartości pól meteorologicznych po 3 godzinach od inicjalizacji obliczeń, musi zostać wykonane bardzo wiele obliczeń pośrednich. Po pierwszym kroku czasowym otrzymuje się wartości pól meteorologicznych w węzłach, które stają się warunkami początkowymi do obliczeń w węzłach siatki pól meteorologicznych w drugim kroku. Proces przebiega tak długo, aż otrzyma się wartości pól meteorologicznych dla określonego czasu. Ze względu na fakt, że różne superkomputery mogą przeprowadzać obliczenia z różna dokładnością, w każdym kolejnym pośrednim kroku obliczeń będą pojawiały się różnice w wartościach obliczanych pól. Skutek jest taki, że otrzymane w wyniku obliczeń przeprowadzonych na dwóch różnych superkomputerach prognozy, na przykład pola ciśnienia, pomimo wykorzystania tego samego modelu będą się nieznacznie różniły (rys. 2).
Kolejnym istotnym zagadnieniem mającym wpływ na wyniku symulacji, jest fakt, że procesy fizyczne zachodzące w atmosferze – dynamiczne i termodynamiczne – opisane są równaniami różniczkowymi. Niestety dla tak złożonych procesów równania te nie posiadają rozwiązań analitycznych. Do rozwiązań równań należy zastosować schematy różnicowe.
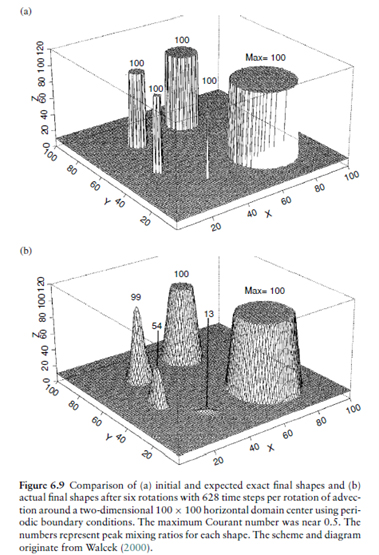
Od schematu różnicowego oczekuje się, aby aproksymował układ różniczkowy oraz w granicach małych kroków w czasie i przestrzeni był identyczny z układem różniczkowym. Gdy ten warunek nie będzie spełniony, schemat różnicowy nie może w żaden sposób symulować zagadnienia warunku początkowego. Dokładność rozwiązania numerycznego, jako aproksymacji rozwiązania równania różniczkowego, pogarsza się w skutek występowania błędów metody, zaokrąglenia oraz w wyniku występowania dyfuzji (rys. 3) i dyspersji numerycznej.
Zmienne ciągłe są reprezentowane zbiorem dyskretnych punktów stanowiących węzły siatki, w których przeprowadzane są obliczenia (rys. 4).
Dane wejściowe pochodzą z punktów pomiarowych, które nie pokrywają się z węzłami siatki numerycznej, co więcej niekoniecznie są równomiernie rozłożone w przestrzeni. W celu uzyskania warunków początkowych w węzłach siatki dokonuje się interpolacji danych pomiarowych na węzły siatki. Czy problem błędów zostałby wyeliminowany, gdybyśmy w każdym węźle siatki mieli stacje pomiarową? Odpowiedź jest natychmiastowa, nie. Jak już zostało wspomniane wcześniej, każdy pomiar obarczony jest niepewnością, która wpływa na symulację. Węzły siatki obliczeniowej znajdują się w pewnej odległości od siebie, zatem siatka numeryczna charakteryzuje się pewną rozdzielczością. Jeżeli odległość między węzłami siatki maleje, to rozdzielczość siatki rośnie. Jak już wspomniano wcześnie, zanim otrzymane zostaną prognostyczne wartości pól meteorologicznych dla terminu prognozy, muszą zostać przeprowadzone obliczenia pośrednie, z pewnym krokiem czasowym. Wielkość kroku czasowego zależała będzie od rozdzielczości modelu, który musi zostać tak dobrany, aby model był stabilny. Czy rozdzielczość siatki numerycznej oraz krok czasowy będzie wpływał na wyniki końcowe? Jeżeli przeprowadzimy prosty eksperyment numeryczny, w którym obliczenia zostaną wykonane na dwóch siatkach obliczeniowych różniących się rozdzielczością, to otrzymane symulacje będą się od siebie różniły. A więc rozdzielczość siatki będzie miała wpływ na końcowe wyniki obliczeniowe. Zmniejszanie kroku czasowy obliczeń oraz zwiększanie rozdzielczości siatki numerycznej powoduje, że otrzymane symulacje są bardziej zbliżone do rzeczywistości. Takie rozwiązania będą bardziej odwzorowywały rzeczywistość. Z kolei zwiększeniu rozdzielczości horyzontalnej siatki oraz zmniejszeniu kroku czasowego towarzyszyć będzie wydłużenie czasu obliczeń. Wówczas potrzebna jest lepsza maszyna o większej mocy obliczeniowej.
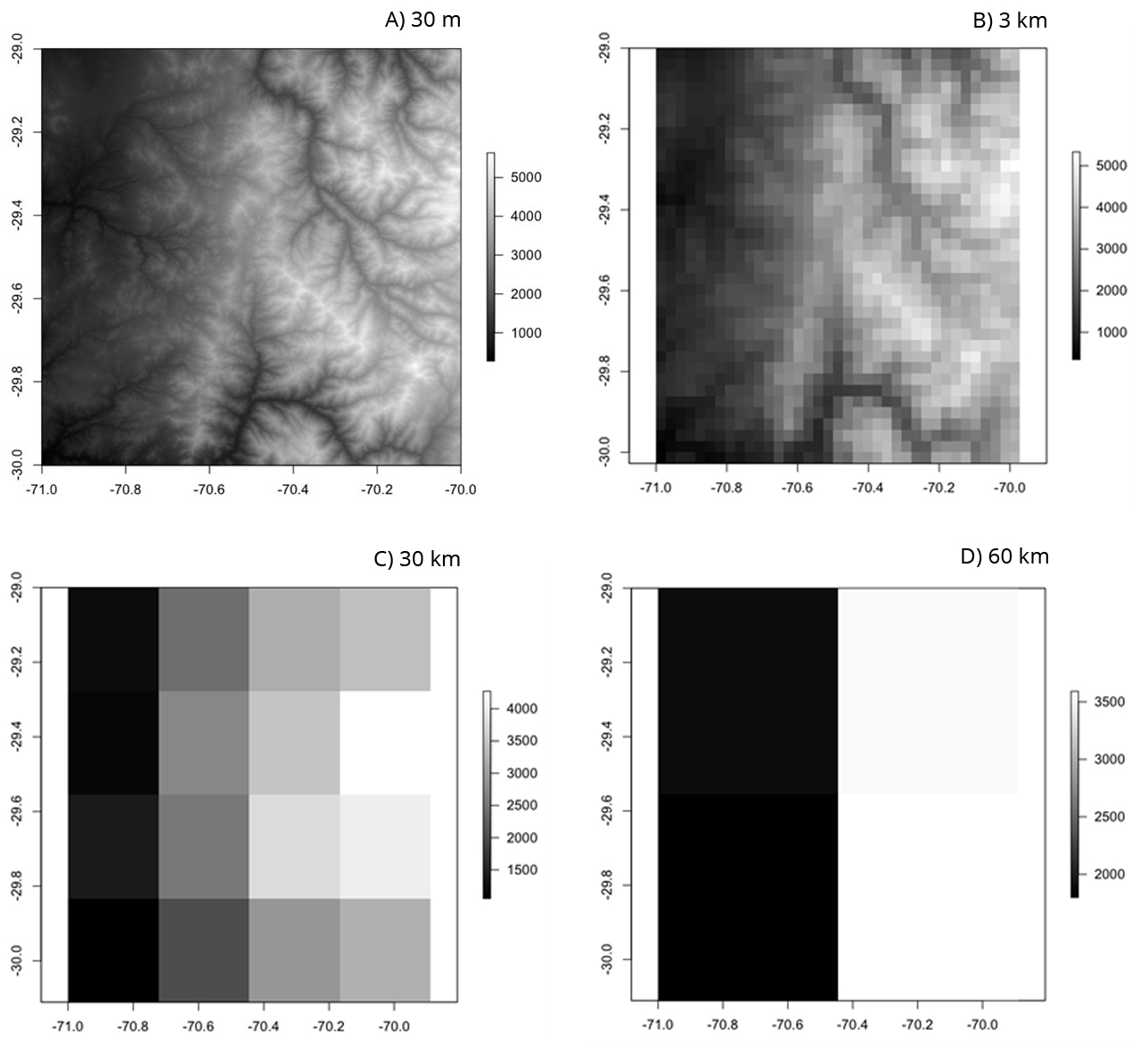
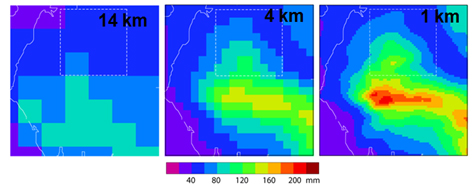
Zwiększaniu rozdzielczości towarzyszy lepsze odwzorowanie lokalnej topografii terenu, co przekłada się na poprawę wyników obliczeniowych. W przypadku złożonej topografii możliwe jest uruchomienie modelu mezoskalowego (lokalnego) w wyższej rozdzielczości, poprzez zagnieżdżanie domeny przy zmniejszającym się rozmiarze komórki, w celu uzyskania bardziej szczegółowej symulacji. W takich symulacjach warunki brzegowe i początkowe z reguły zapewniają modele globalne o rozdzielczościach z przedziału 0p25 do 1p00 stopnia, które przenoszą jednocześnie błędy w nich zawarte do modeli mezoskalowych. Modele regionalne o wysokiej rozdzielczości, szczególnie istotne dla obszarów górskich, ale nie tylko, pozwalają na lepszą symulację na przykład przepływu mas powietrza w obszarze ze złożoną topografią. Przy rozdzielczości rzędu 0p25 lub 0p50 modele globalne nie przedstawiają dokładnie pasm górskich, pomijają najwyższe góry i wniesienia nawet o tysiące metrów. Dlatego wręcz konieczne jest zmniejszenie skali wyników przy użyciu modeli, które mogą obejmować mniejszy obszar, ale w wyższej rozdzielczości. Na rysunku 5 przedstawiono przykład, jak wraz ze spadkiem rozdzielczości następuje zmniejszenie wysokości i wygładzanie rzeźby terenu. Modele meteorologiczne o niższej rozdzielczości nie są w stanie rozróżnić wpływu gór na opady, opór wiatru i wiele innych parametrów meteorologicznych i dlatego są mniej wiarygodne niż modele o wyższej rozdzielczości.
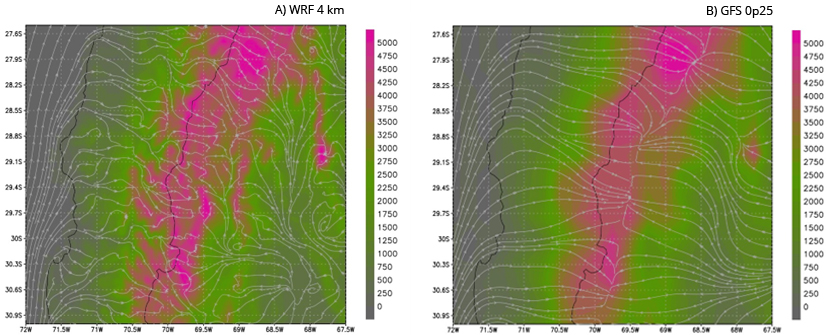
Różnice w rozdzielczości użytego numerycznego modelu terenu mają duży wpływ podczas modelowania prędkości wiatru, jak pokazano na rysunku 6. Po lewej stronie mamy wynik prognozy z modelu WRF o rozdzielczości 3 m, na którym można zidentyfikować poszczególne doliny oraz to, jak strumienie wiatru podążają zgodnie z różnymi formami ukształtowania terenu. To z kolei ma wpływ na prędkość wiatru, a tym samym przekłada się na jakość prognoz energii farm wiatrowych.
Zwiększenie rozdzielczości siatki obliczeniowej wpływa także na proces upraszczania procesów fizycznych zachodzących w atmosferze.
Upraszczanie procesów (parametryzacja procesów podskalowych)
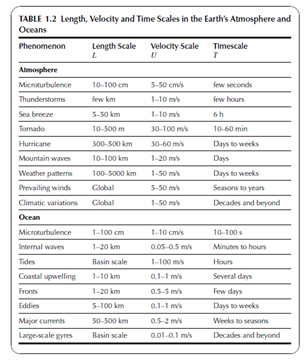
W atmosferze zachodzi wiele złożonych procesów fizycznych i to w wielu skalach (rys. 7, 8). Procesy zachodzące w skali mniejszej niż rozdzielczość siatki numerycznej, czyli tzw. procesy podskalowe, muszą być parametryzowane, co oznacza, że tworzy się uproszczone modele, które reprezentują statystycznie uśrednione efekty tych procesów. W modelach numerycznych parametryzuje się m.in. procesy radiacyjne, procesy mikrofizyczne zachodzące w chmurach, procesy zachodzące w warstwie granicznej, konwekcję itd. Problemem pozostaje także dobre odwzorowanie powierzchni ziemi, wraz z prawidłowym rozkładem obszarów pokrytych roślinnością lub jej brakiem. Bardzo istotnym zagadnieniem jest prawidłowo ujęty rozkład rodzajów gleby, głębokości ukorzenienia roślin itp., ponieważ charakterystyki te mają istotny wpływ na procesy termiczne i hydrologiczne w profilu glebowym, a w rezultacie na strumienie ciepła, wilgotności i pędu na styku atmosfera-powierzchnia ziemi. Każda zmiana zachodząca w sposobie użytkowania terenu wpływa na lokalny bilans promieniowania oraz przepływ powietrze w warstwie granicznej (a ludzie zmieniają krajobraz w zasadzie w trybie ciągłym, szczególnie w obrębie aglomeracji miejskich lub w pobliżu dużych inwestycji inżynierskich). W żadnym z obecnie istniejących numerycznych modeli pogody nie ma możliwości wprowadzania zmian w trybie ciągłym.
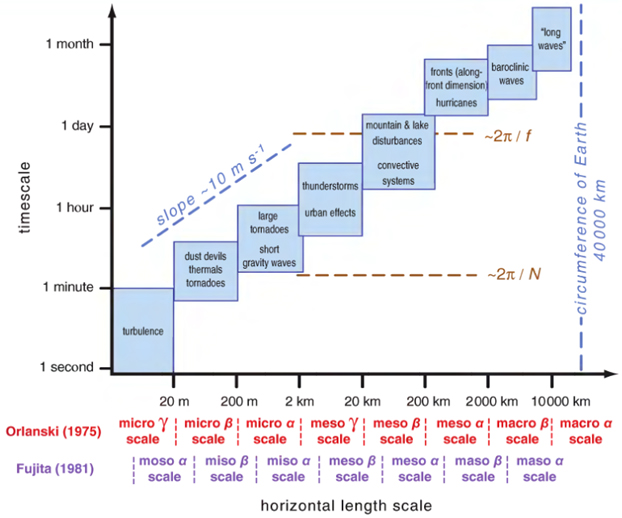
Zwiększenie rozdzielczości siatki obliczeniowej powoduje, że niektóre procesy, które były procesami podskalowymi i musiały być parametryzowane, przy zwiększonej rozdzielczości będą jawnie reprezentowane. Przykładem niech będzie zjawisko konwekcji. W modelach, których rozdzielczość siatki numerycznej była np. powyżej 15 km, procesy te musiały być parametryzowane. W modelach mezoskalowych o rozdzielczości np. 2,8 km głęboka konwekcja jest jawnie reprezentowana w skali siatki numerycznej. Takie modele nazywane są modelami konwekcyjno-skalowymi. Przy takiej rozdzielczości jedynie płytka konwekcja musi być nadal parametryzowana.
Prognoza pogody w zależności od modelu NWP
Każdy odbiorca prognoz meteorologicznych spostrzegł podczas przeglądania prognoz meteorologicznych z różnych modeli, że nieco się one różnią. Ponownie pojawia fundamentalne pytanie dlaczego? Odpowiedź na to pytanie jest prosta. Każdy numeryczny model meteorologiczny różni się od siebie m.in. rodzajem zastosowanych siatek obliczeniowych, rozdzielczością horyzontalną siatki i różnymi parametryzacjami opisującymi te same procesy fizyczne. Przykładem niech będą procesy mikrofizyczne zachodzące w chmurach. Jeśli przyjrzymy się schematowi z rys. 10, zauważymy jak wiele procesów mikrofizycznych musi zajść w chmurze zanim powstanie opad.
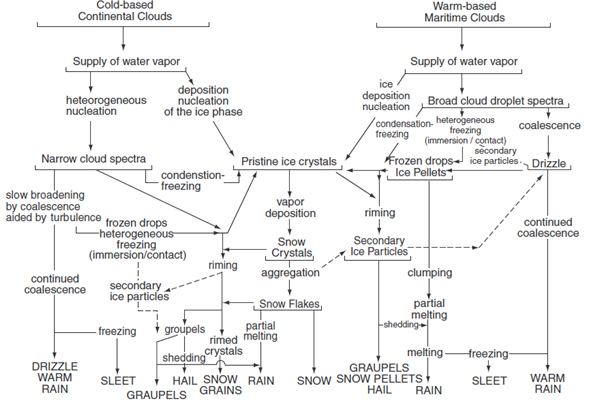
W celach poglądowych rozważmy opad deszczu w schemacie z jedną kategorią lodu (rys. 11).
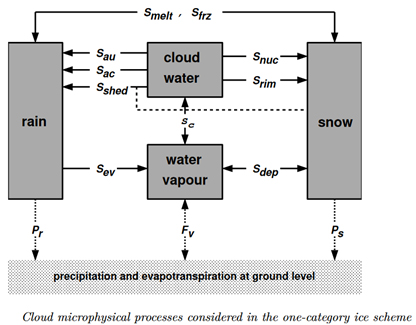
W schemacie mamy fazę mieszaną chmury złożoną z:
a) pary wodnej;
b) wody chmurowej;
c) deszczu;
d) śniegu.
Opad deszczu niech zostanie zapisany symbolicznym równaniem:
Opad deszczu = –Sev + Sau + Sac + Smelt – Sfrz + Sshed
Przez symbol „S” rozumieć należy procesy fizyczne, które dają wkład do opadu deszczu. Ponieważ procesy te zachodzą w skali mniejszej niż rozdzielczość siatki obliczeniowej, muszą być parametryzowane. A więc w tym wypadku jest ich aż sześć. Kiedy sięgnie się do literatury przedmiotu, zauważymy, że każdy proces mikrofizyczny może być parametryzowany na kilka różnych sposobów. W poszczególnych modelach numerycznych mogą byś zaimplementowane różne parametryzacje opisujące ten sam proces mikrofizyczny. Zatem opady prognozowane przez poszczególne modele mogą się różnić od siebie (rys. 12). Podobnie jest z innymi procesami fizycznymi, które muszą być parametryzowane.
Prognozy wiązkowe
Mając na uwadze ograniczenia numerycznego modelu pogody, zaproponowano wielokrotne uruchamianie modelu z różnego stanu początkowego (ze względu na niepewności pomiarowe) (rys. 14), z inną fizyką (z różnymi parametryzacjami np. konwekcji) lub numeryką (z wykorzystaniem różnych numerycznych schematów obliczeniowych). Celem takich działań jest oszacowanie niepewności prognozy. Jak wskazują badania naukowe, prognoza otrzymana w wyniku uśrednienia prognozy po wszystkich elementach wiązki ma większa sprawdzalność niż prognoza deterministyczna.
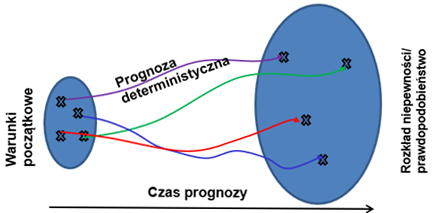
Prognozy wiązkowe pozwalają m.in. ocenić, z jakim prawdopodobieństwem wydarzy się dane zjawisko, np. opad marznący.
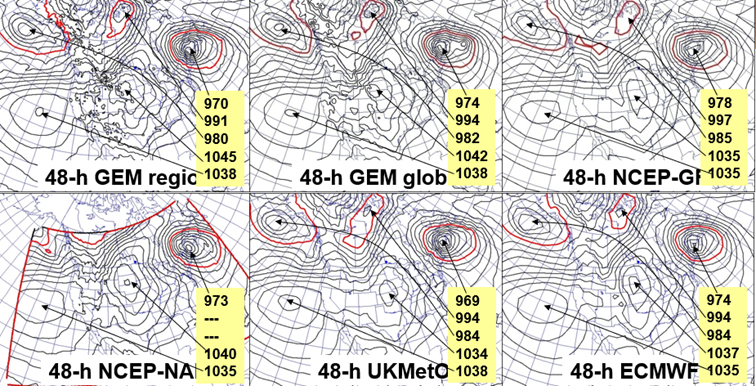
Elementy wiązki ad hoc można także otrzymać w wyniku przeprowadzenia obliczeń na różnych superkomputerach lub elementy wiązki otrzymuje się wykorzystując różne modele (rys. 17).
Użyteczność numerycznych modeli pogody
Widząc jak duży jest potencjał błędów w numerycznych modelach pogody, można dojść do wniosku, że prognozy numeryczne są bezużyteczne. Oczywiście tak podszedłby do zagadnienia odbiorca prognoz pogody bez odpowiedniego przygotowania merytorycznego. Natomiast doświadczeni synoptycy, którzy znają mocne i słabe strony modeli pogody, uważają je za bardzo przydatne (obecnie niezbędne) narzędzie w prognozowaniu pogody. Wiedzą o ich niedoskonałościach i dlatego podczas opracowywania prognozy korzystają z wyników obliczeń numerycznych, których źródłem jest kilka innych modeli. Ponadto odbiorcom, w tym także i synoptykom dostarczane są prognozy wiązkowe. Korzystanie z takiego zespołu modeli pogodowych pomaga meteorologom lepiej zrozumieć proces ewolucyjny procesów dynamicznych i termodynamicznych zachodzących w atmosferze, a także z większą trafnością zaprognozować scenariusz zachodzących procesów fizycznych w atmosferze, czyli przyszłych warunków meteorologicznych.
Każdy odbiorca musi być świadomy, że prognoza pogody przedstawia jedynie prawdopodobny scenariusz pogodowy, który nie jest żadnym pewnikiem. W sytuacji kiedy spodziewamy się wystąpienia groźnego zjawiska, należy dość często sprawdzać prognozy i je analizować.
Wraz z rozwojem wiedzy z zakresu fizyki atmosfery oraz postępem technologicznym pozwalającym tworzyć maszyny o coraz większej mocy obliczeniowej, jakość prognoz numerycznych będzie się poprawiała. Należy mieć jednak świadomość, że nigdy nie uda się otrzymać prognoz, które będą miały 100 proc. sprawdzalność, tym bardziej w przypadku prognoz z długim horyzontem czasowym.
Należy mieć na uwadze, że sama ocena sprawdzalności prognoz nie jest trywialnym zadaniem. Ze względu na opisane wcześniej aspekty numeryczne, wartości modelowanych parametrów w dwóch sąsiednich węzłach modelu są bardziej skorelowane niż dla dwóch stacji pomiarowych będących w takiej samej odległości od siebie. Jest to szczególnie widoczne w przypadku opadów. Z tego względu unika się bezpośredniego porównywania wyników modeli numerycznych do pomiarów na najbliższej stacji i stosuje się metody statystyczne, pozwalające na zminimalizowanie wpływu niejednorodności sieci pomiarowej czy jej gęstości.
Sprawdzalność numerycznych prognoz pogody
Obecne prognozy siedmiodniowe mogą dokładnie przewidzieć pogodę w około 80 proc. przypadków, a prognozy pięciodniowe – w około 90 proc. przypadków. Jednak prognoza 10-dniowa lub dłuższa sprawdza się już tylko w 50 proc.
Obliczenia numeryczne inicjowane są, w zależności od możliwości technicznych narodowych służb meteorologicznych, raz, dwa, cztery lub więcej razy na dobę. Przy każdej inicjalizacji model wykorzystuje inne dane wejściowe. Skutkuje to tym, że każde kolejne symulacje stanu atmosfery, w zależności od sytuacji synoptycznej, będą się mniej lub bardziej różniły od siebie. I jest to naturalne. Zatem oczekiwanie, że w wyniku każdego kolejnego przebiegu modelu otrzyma się identyczny scenariusz przebiegu procesów fizycznych w atmosferze jest błędne. W wypadku prognoz krótkoterminowych kolejne symulacje aż tak znacząco się nie będą różniły od siebie. Wraz z wydłużaniem się horyzontu czasu prognozy (np. prognozy średnioterminowe), różnice w symulacji będą się zwiększały.
Zdjęcie główne: Marc Thunis | Unsplash.